For helping students in efficiently and strictly programming loops, we propose a graphical programming methodology relying on the Loop Invariant ((a program loop property verified at each iteration — i.e., at each evaluation of the Loop Condition). This methodology is applied in the context of our Introduction to Programming (i.e., CS1) course alternating between specific C programming language concepts and algorithmic aspects. In particular, the course aims at introducing to first year students basic principles of programming. The concept of a correct and efficient algorithm is highlighted, in the context of a strict programming methodology. Typically, an algorithm requires to write a sequence of instructions that must be repeated a certain number of times. This is usually known as a program loop. The methodology we teach for programming a loop is based on an informal version of the Loop Invariant introduced by Floyd and Hoare. Our methodology consists in determining a strategy (based on the LoopInvariant) to solve a problem prior to any code writing and, next, rely on the strategy to build the code, as initially proposed by Dijkstra.
As such, the Loop Invariant can be seen as the cornerstone of code writing. However, the issue is that it relies on an abstract reflection that might confuse students who may not have the desired abstract background, specially if the Loop Invariant is expressed as a logical assertion.
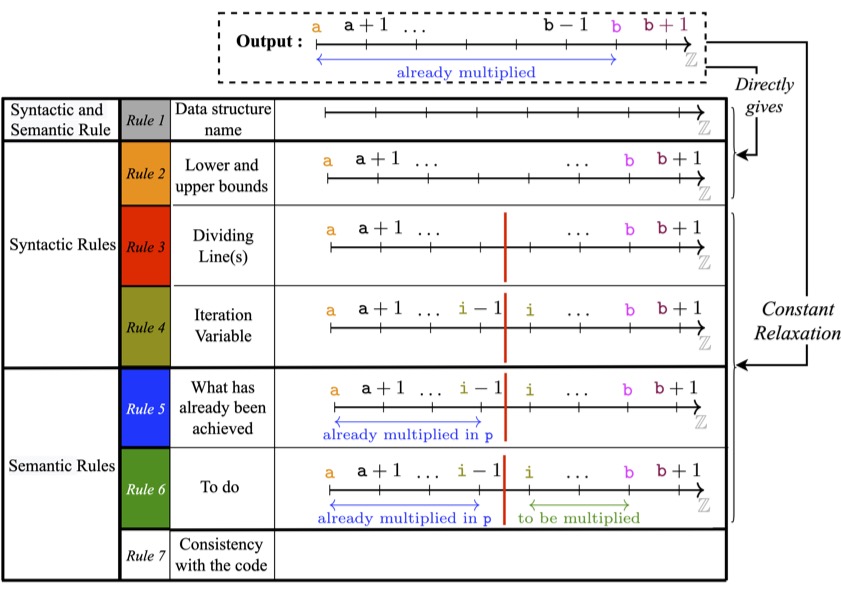
To ensure students follow a strict programming methodology despite their (potential) gaps, we propose a Graphical Loop Invariant (GLI — see the figure above illustrating the process of building a GLI for the problem of multiplying all integers in the range [a,b]). The GLI informally describes, at least, variables, constant(s), and data structures handled by the program; their properties; the relationships they may share, and that are preserved over all the iterations. The goal behind is to generalize what the program must have performed after each iteration. In addition to natural advantages of drawings, the GLI allows the programmer to visually deduce instructions before, during, and after the loop. That approach forges abstraction skills without relying on any mathematical background and lays the foundations for more formal methods where the GLI stands as an intermediate step towards a final formal Loop Invariant (being a logical assertion).
The course provides students with predefined drawing patterns (number line, numbers, terminal, array, etc.) and a set of rules (see rules 1 → 6 on the figure above) for systematically and formally build their GLI).
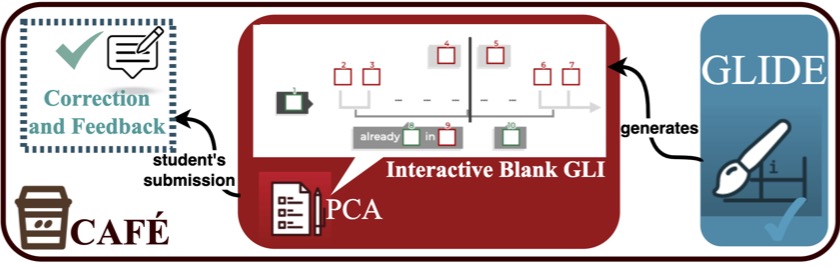
Our programming methodology is supported by the PCA activity and GLIDE, both running on top of CAFÉ 2.0, as illustrated above. To ensure an automatic correction of Programming Challenges on CAFÉ 2.0, students are exposed to an interactive blank GLI they have to complete based on existing proposals (green boxes below) or according to their variables/expressions needs (red boxes below). That drawing is then manipulated to build the code, in a sequence of steps managed by CAFÉ 2.0. GLIDE is used by students for practicing GLI.
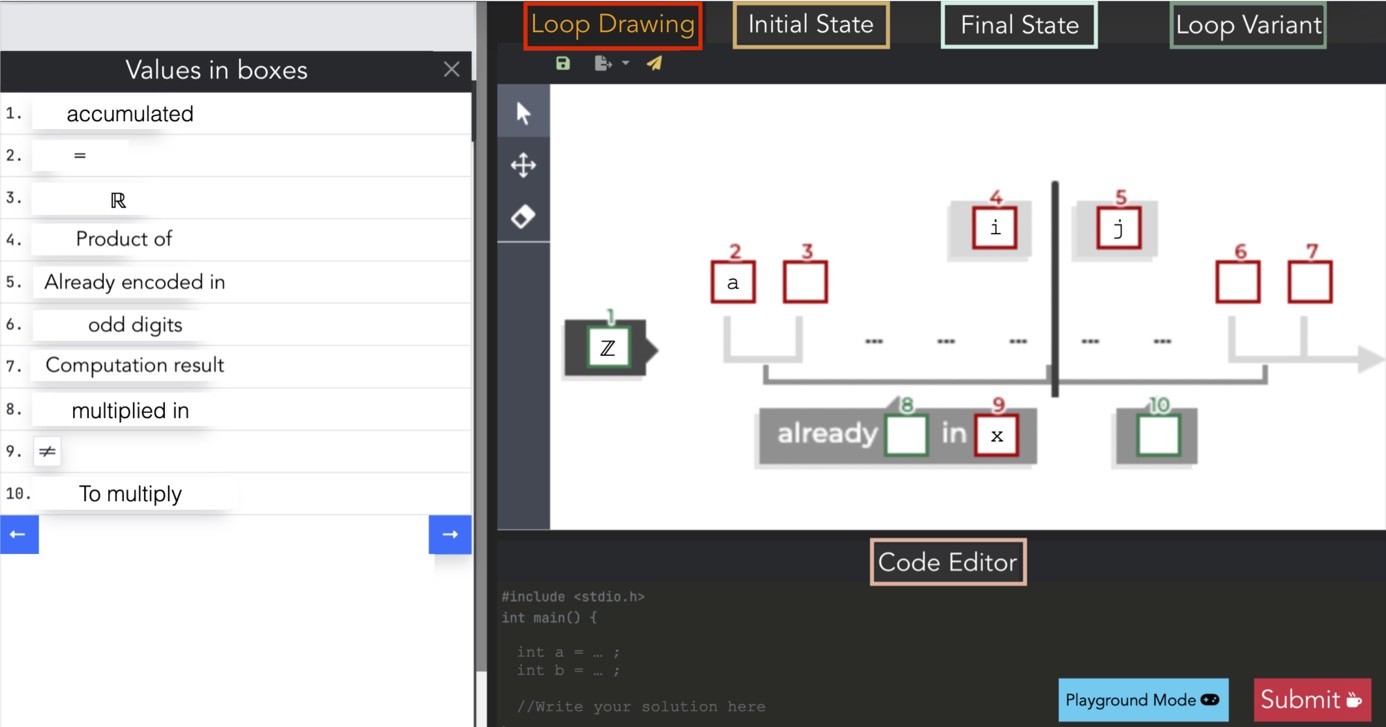
Although thinking through drawing is more intuitive and requires less formalization, it also relies on diagrammatic reasoning, which involves abstraction and is therefore an important competence in STEM.