The Graphical Loop Invariant Drawing Editor (GLIDE) guides students in drawing their GLI by using the predefined graphical patterns and following the building rules. GLIDE is illustrated below. On the top-left, you can notice a drop-down list itemizing the different drawing patterns. Once a student has selected the appropriate one, they can start formally describing their loop mechanism according to the first six rules. The graphical components the student can use are available on the left. Each of them is mapped to one/several rule(s).
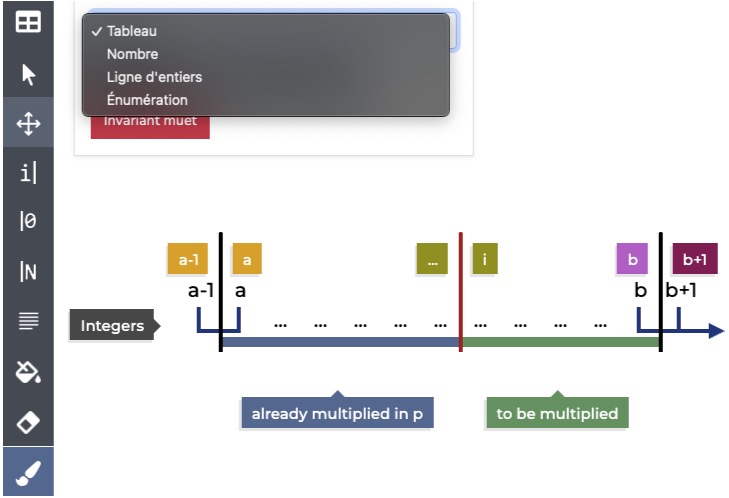
Once a student considers their GLI is completed, they can submit it and some basic checks are performed. In particular, syntactic mistakes are detected (such as the lower bound being further than the upper bound or some description of what has been achieved so far that is missing). However, the GLI semantic is not verified, which means that the solution can be positively assessed by the GLIDE while the GLI does not make sense.
GLIDE also allows the educational team to produce interactive blank GLI (bGLI), i.e., a canvas the students have to fill out. Such a blank drawing depicts only the general shape a correct and rigorous GLI should follow (i.e., the predefined graphical pattern) in response to a given problem. Students must then annotate properly the canvas so that the drawing becomes the figure of their Loop Invariant for their solution to the particular problem to be solved.
Any bGLI always comes with two types of box: (i) red boxes standing to host expressions (i.e., constants, variables, operations, or left blank) and are to be completed by students without support; (ii) green boxes standing to host labels that students must drag and drop from a pre-defined list. That list contains multiple choices, some of them being the expected answers, others being purely random. Doing so, we pave the way for an automatic correction of the GLI (with strong feedback). This can be achieved thanks to the fact each box is numbered. In this way, when a student’s solution gets corrected, each piece of solution is easy to be pointed out, allowing to bring a rich feedback while still keeping it clear and smooth to digest for the student. That process is supported by CAFÉ 2.0 in the context of Programming Challenges.